(三)最优化建模与算法之基础知识_IM-IM电竞真空泵水泵销售中心

当前位置：首页 > 新闻中心 > (三)最优化建模与算法之基础知识

(三)最优化建模与算法之基础知识

时间：2024-09-09 13:54:05 点击次数：

作为工科生，将手中的物理实际问题抽象成优化问题，那么问题就基本解决了99%了，剩下的就可以交给数学和计算机了。最优化问题（Optimization problem）在数学与计算机科学领域中，是从所有可行解（feasible solution）中寻找最优良的解的问题。

最优化问题(也称优化问题)泛指定量决策问题，主要关心如何对有限资源进行有效分配和控制，并达到某种意义上的最优。通常对问题进行定性和定量分析，建立恰当的数学模型来描述该问题，设计合适的计算方法来寻找问题的最优解，探索研究模型和算法的理论性质，考察算法的计算性能等。由于很多数学问题难以直接给出显式解，最优化模型就成为人们最常见的选择，计算机的高速发展也为最优化方法提供了有力辅助工具。

最优化问题一般可以描述为： $\\mathrm{min}\\quad f(x), \\mathrm{s.t.}\\quad x \\in \\mathcal{X}\ ag{1}$

其中 $x=(x_1,x_2,\\cdots, x_n)^T \\in \\mathbb{R}^n$ 为决策变量(空间列向量，也可以为矩阵或张量等)， $f:\\mathbb{R}^n\\rightarrow \\mathbb{R}$ 为目标函数， $\\mathcal{X}\\subseteq \\mathbb{R}^n$ 为约束几何或可行域，可行域包含的点称为可行解。 $\\mathrm{s.t.}$ 为"subject to"的缩写，为约束条件。当 $\\mathcal{X}=\\mathbb{R}^n$ 时，上式为无约束优化问题。约束条件通常可以表示成下式：

$\\mathcal{X}=\\{ x\\in \\mathbb{R}^n| c_i(x)\\leq0,i=1,2,\\cdots,m,c_j(x)=0,j=m+1,m+2,\\cdots,m+l \\}\ ag{2}$

约束条件包含 $m$ 个不等式约束和 $l$ 个等式约束条件。在满足上述约束条件的决策变量中，使式(1)取最小值的变量 $x^\\ast$ 为优化问题的最优解。

注：优化问题为求最大值和目标函数的最小值(最大值)不存在时，可以分别用下式进行最小化问题转化和求问题的确界： $\\begin{cases}\\mathrm{max}\\ f=\\mathrm{min}\\ -f \\\\ \\mathrm{min(max)}\\ f=\\mathrm{inf(sup)}\\ f \\end{cases}\ ag{3}$

常见优化分类介绍：

线性规划：目标函数和约束形式均为线性函数；
非线性规划：目标函数和约束形式至少有一个非线性函数；
二次规划：目标函数为二次函数，约束函数为线性函数；
整数规划：变量只能取整数的优化问题；
半正定规划：在线性约束下极小化关于半正定矩阵的线性函数的问题，其广义形式为锥规划；
稀疏优化：最优解只有少量非零元素的问题；
低秩矩阵优化：最优解是低秩矩阵的问题。

此外还有几何优化、二次锥规划、张量优化、鲁棒优化、全局优化、组合优化、网络规划、随机优化、动态规划、带微分方程约束优化、微分流形约束优化、分布式优化等。

优化问题具体应用涵盖统计学习、压缩感知、最优运输、信号处理、图像处理、机器学习、强化学习、模式识别、金融工程、电力系统等领域的优化模型。

稀疏优化：稀疏优化是求解线性欠定(无穷多个解)方程组的方法，加入稀疏先验信息来约束解空间，稀疏先验的形式有很多种，比如拉普拉斯(压缩感知)、独立高斯(稀疏贝叶斯学习)等。稀疏特性是符合自然世界规律的，比如财富由少数人掌握，物体(目标)几个主要部分构成的等，因此只需要关注这些核心关键要素，即稀疏点，这也类似哲学所描述抓住事物的主要矛盾。

这里不在详细介绍稀疏优化，感兴趣可参考稀疏优化在雷达ISAR成像中的应用：

https://zhuanlan.zhihu.com/p/610244077

以一范数和二范数约束为例，仿真结果如下图所示：

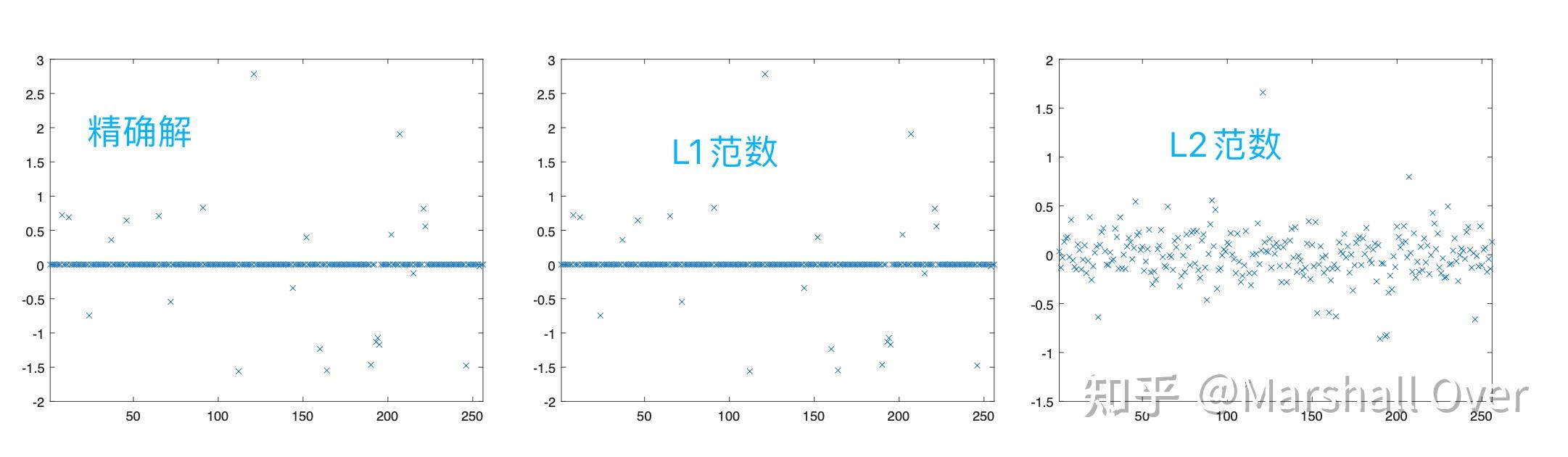
产生这种现象可以从三个方面来解释：

概率解释：1范数对应拉普拉斯先验，而拉普拉斯概率密度函数在0处很大，且下降极其快(导数大)，故保证解稀疏的；
几何解释：如下图所示，解更容易落在坐标轴上；
优化解释：1范数优化求解器中涉及到求导，读者可自行脑补。

产生稀疏解的几何解释如下图所示：

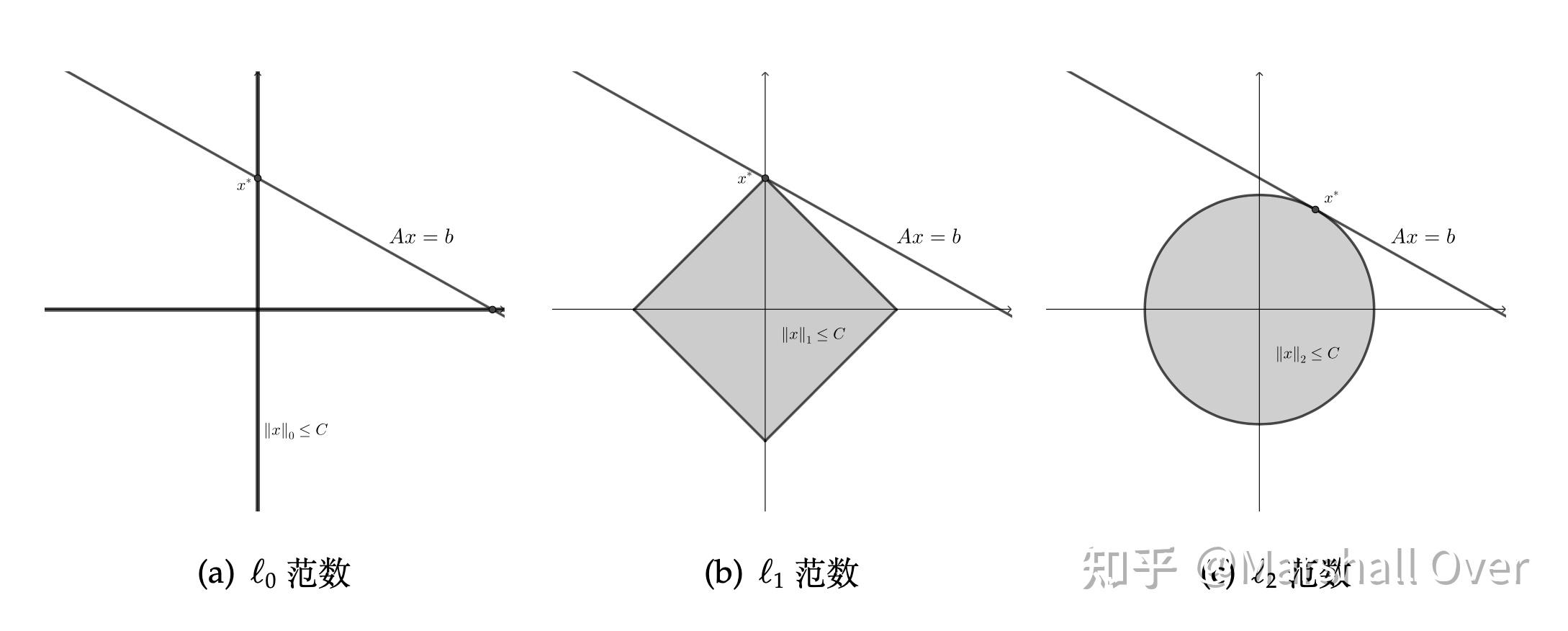
一般来说，最优化算法研究可以分为：构造最优化模型、确定最优化问题的类型和设计算法、实现算法或调用优化算法软件包进行求解。

最优化问题可以分为连续和离散优化问题两大类。连续优化问题是指决策变量所在的可行集合是连续的，比如平面、区间等。离散优化问题是指决策变量能在离散集合上取值，比如离散点集、整数集等。常见的离散优化问题有整数规划，其对应的决策变量的取值范围是整数集合。

在连续优化问题中，基于决策变量取值空间以及约束和目标函数的连续性，从一个点处目标和约束函数的取值来估计该点可行邻域内的取值情况，进一步地，可以根据邻域内的取值信息来判断该点是否最优。离散优化问题则不具备这个性质，因此在实际中往往比连续优化问题更难求解．实际中的离散优化问题往往可以转化为一系列连续优化问题来进行求解。如下图所示：

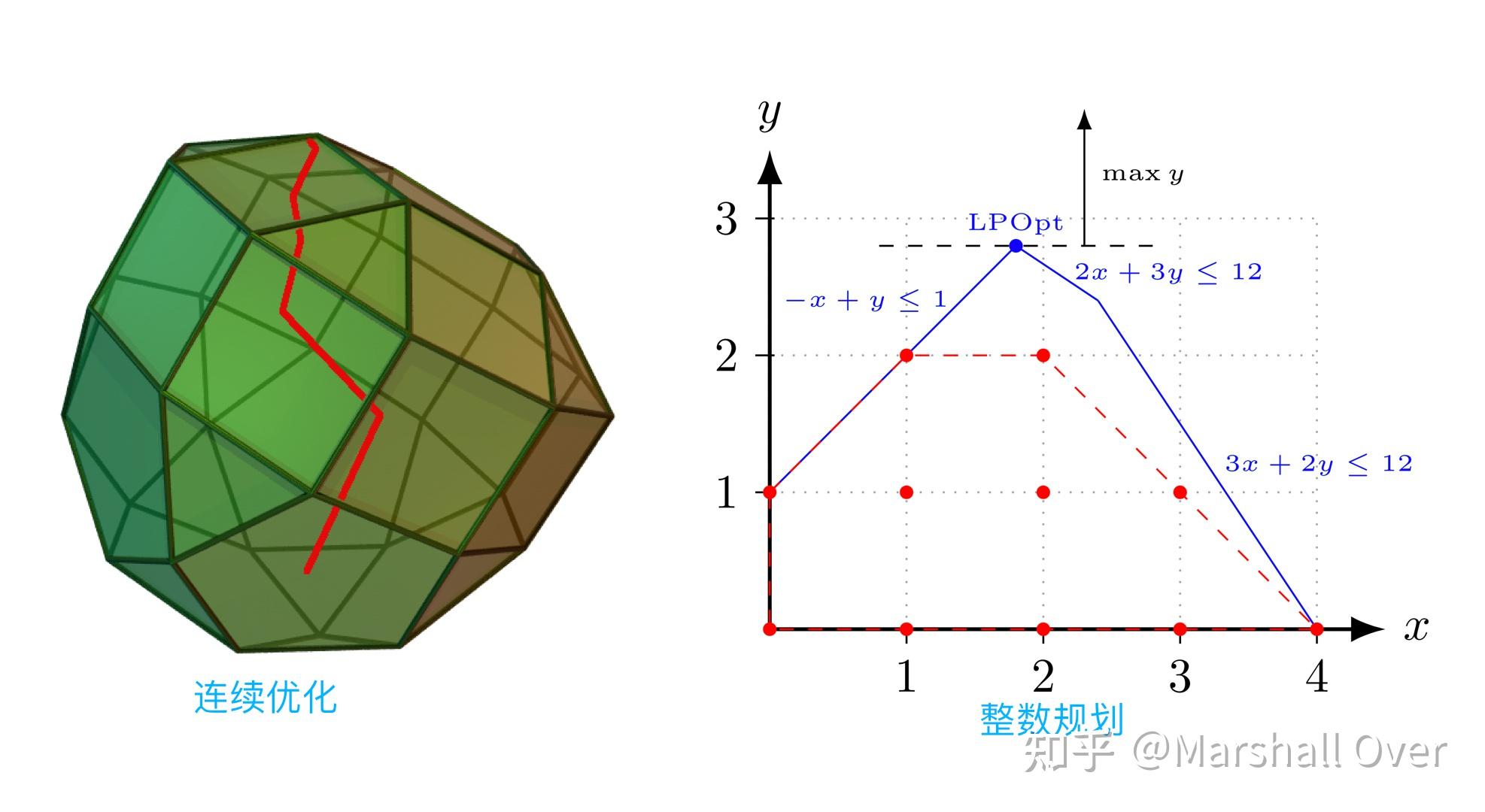
最优化问题的另外一个重要的分类标准是约束是否存在。无约束优化问题的决策变量没有约束条件限制。一般约束优化比无约束优化复杂，这也是经常利用拉格朗日乘子方法将约束优化问题转化成无约束优化问题的原因。

随机优化问题是指目标或者约束函数中涉及随机变量而带有不确定性的问题，包含一些未知的参数。确定性优化问题中目标和约束函数都是确定的。随机优化问题在机器学习、深度学习以及强化学习中有着重要应用，其优化问题的目标函数是关于一个未知参数的期望的形式，通常通过足够多的样本来逼近目标函数，得到一个新的有限和形式的目标函数，进行随机优化求解。Fluctuations in the total objective function as gradient steps with respect to mini-batches are taken：

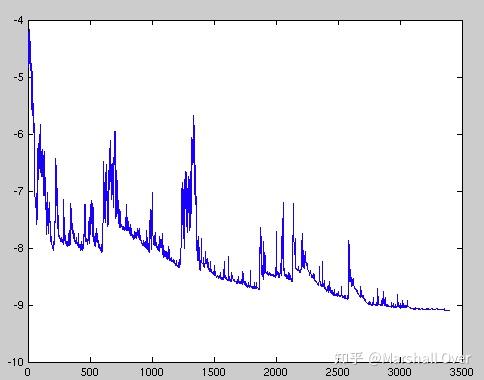
线性规划是指目标函数和约束函数都是线性的。当目标函数和约束函数至少有一个是非线性的，那么对应的优化问题的称为非线性规划问题。类似于连续函数可以用分片线性函数来逼近一样，线性规划问题的理论分析与数值求解可以为非线性规划问题提供很好的借鉴和基础。

在1946—1947 年，George Bernard Dantzig 提出了线性规划的一般形式，并提出了至今仍非常流行的单纯形方法。虽然单纯形方法在实际问题中快速收敛，但其复杂度并不是多项式的。1979 年，Leonid Khachiyan 证明了线性规划问题多项式时间算法的存在性。1984 年，Narendra Karmarkar 提出了多项式时间的内点法，内点法也被推广到求解一般的非线性规划问题。目前，求解线性规划问题最流行的两类方法依然是单纯形法和内点法。

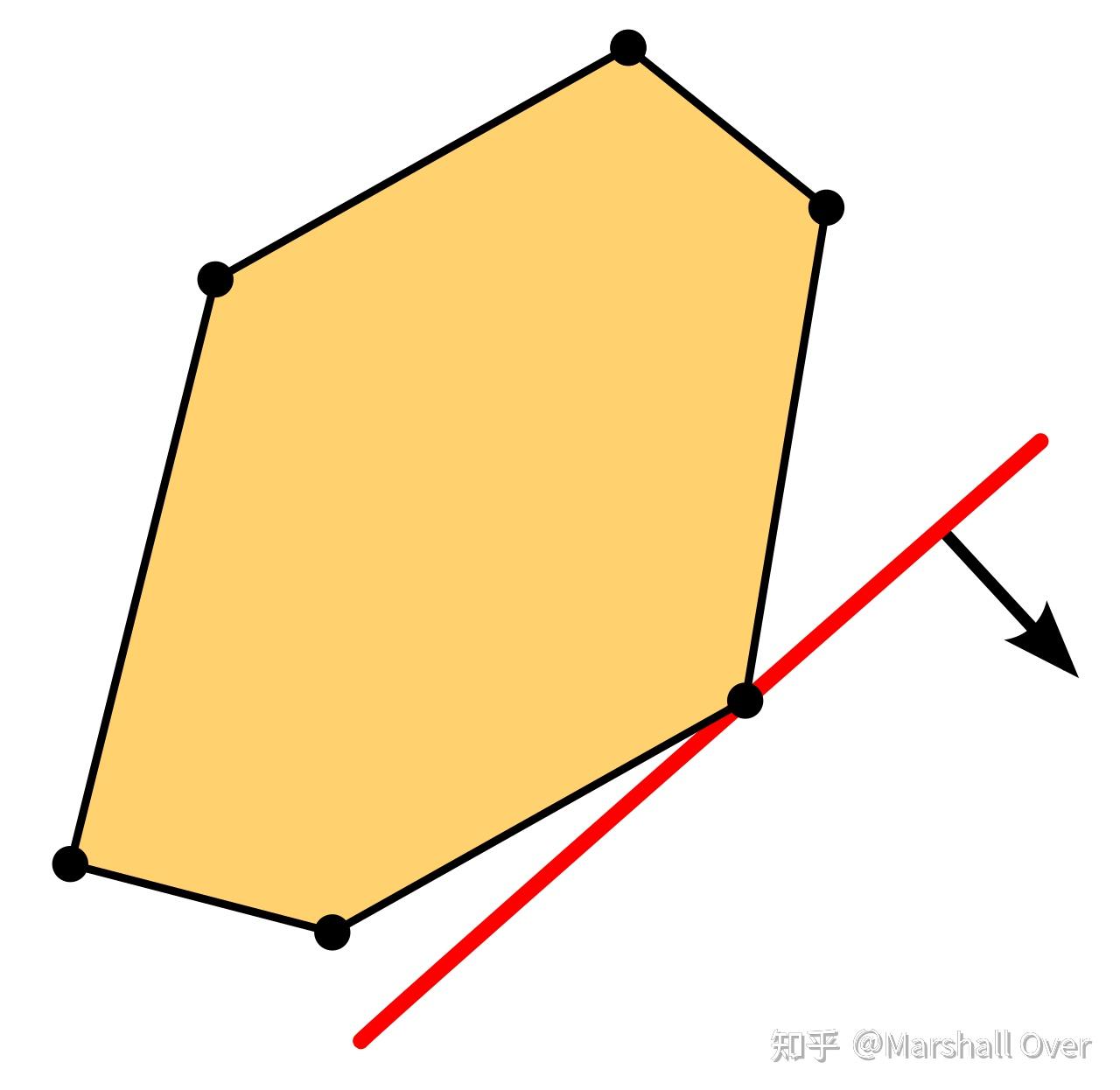
凸优化问题是指目标函数和可行域分别是凸函数和凸集。如果其中有一个或者两者都不是凸的，那么相应的最小化问题是非凸优化问题。因为凸优化问题的任何局部最优解都是全局最优解，其相应的算法设计以及理论分析相对非凸优化问题简单很多。

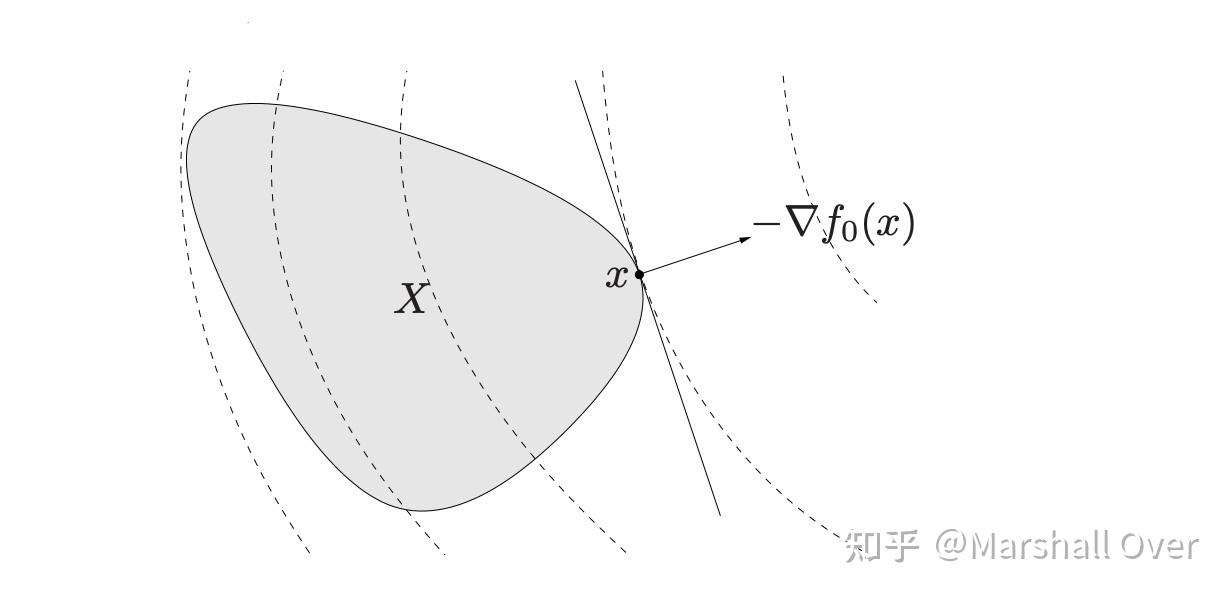
在给定优化问题之后，根据优化问题的不同形式，其求解的困难程度可能会有很大差别。对于一个优化问题，如果能用代数表达式给出其最优解，那么这个解称为显式解，对应的问题往往比较简单。但实际问题往往是没有办法显式求解的，因此常采用数值迭代算法。

迭代算法的基本思想是：从一个初始点出发，按照某种给定的规则进行迭代，得到一个序列。如果迭代在有限步内终止，那么希望最后一个点就是优化问题的解。如果迭代点列是无穷集合，那么希望该序列的极限点（或者聚点）则为优化问题的解。为了使算法能在有限步内终止，一般会通过一些收敛准则来保证迭代停在问题的一定精度逼近解上。

对于无约束优化问题，常用的收敛准则，包含对目标函数变化和对梯度大小约束如下：

$\\frac{f(x^k)-f^{\\ast}}{\\mathrm{max}\\{|f^{\\ast}|,1 \\}}\\leq \\varepsilon_1,||\\bigtriangledown f(x^k)||\\leq \\varepsilon_2 \ ag{4}$

对于约束优化问题，还需要考虑约束违反度，具体地，要求得到的点满足：

$c_i(x^k)\\leq \\varepsilon_3,c_j(x^k)\\leq \\varepsilon_4,i=1,2,\\cdots,m,j=m+1,\\cdots m+l \ ag{5}$

对于一个具体的算法，不一定能得到高精度的逼近解，为了避免无用的计算开销，需要一些停机准则来停止算法的进行，如 $\\frac{||x^{k+1}-x^k||}{\\mathrm{max}\\{||x^k||,1 \\}}\\leq \\varepsilon_5,\\frac{|f(x^{k+1})-f(x^k)|}{\\mathrm{max}\\{|f(x^k)|,1 \\}}\\leq \\varepsilon_6 \ ag{6}$

上面的准则分别表示相邻迭代点和其对应目标函数值的相对误差很小。在算法设计中，这两个条件往往只能反映迭代点列接近收敛，但不能代表收敛到优化问题的最优解。

在设计优化算法时，对于复杂的优化问题，基本的想法是将其转化为一系列简单的优化问题（其最优解容易计算或者有显式表达式）来逐步求解。

泰勒（Taylor）展开：对于一个非线性的目标或者约束函数，通过其泰勒展开用简单的线性函数或者二次函数来逼近，从而得到一个简化的近似问题。因为该简化问题只在小邻域内逼近原始问题，所以我们需要根据迭代点的更新来重新构造相应的简化问题。

对偶转化：每个优化问题都有对应的对偶问题。特别是凸优化问题，当原始问题比较难解的时候，其对偶问题可能很容易求解。通过求解对偶问题或者同时求解原始问题和对偶问题，可以简化原始问题的求解，从而设计更有效的算法。比如SVM求解。

变量拆分：对于一个复杂的优化问题，我们可以将变量进行拆分。通过引入更多的变量，我们可以得到每个变量的简单问题（较易求解或者解有显式表达式），从而通过交替求解等方式来得到原问题的解。如

$\\mathop{\\min}_{x}\\ h(x)+r(x)\\Rightarrow \\mathop{\\min}_{x,y}\\ h(x)+r(y), \\mathrm{s.t.}\\ x=y \ ag{7}$

块坐标下降: 对于一个n 维空间（n 很大）的优化问题，可以通过逐步求解分量的方式将其转化为多个低维空间中的优化。如：

$\\mathop{\\min}_{x_1,x_2,\\cdots,x_n}\\ h(x) \\Rightarrow \\begin{cases}\\mathop{\\min}_{x_1+\\Delta x_1,x_2,\\cdots,x_n}\\ h(x) \\\\ \\mathop{\\min}_{x_1,x_2+\\Delta x_2,\\cdots,x_n}\\ h(x) \\\\ \\cdots \\\\ \\mathop{\\min}_{x_1,x_2,\\cdots,x_n+\\Delta x_n}\\ h(x) \\\\ \\end{cases}\ ag{8}$

在设计和比较不同的算法时，另一个重要的指标是算法的渐进收敛速度。以点列的Q-收敛速度（Q 的含义为“quotient”）为例。

算法（点列）是Q-线性收敛：满足下式 $\\lim_{k\ o \\infty}\\frac{||x^{k+1}-x^{\\ast}||}{||x^k-x^{\\ast}||}\\leq a, a \\in(0,1)\ ag{9}$

算法（点列）是Q-超线性收敛：满足下式 $\\lim_{k\ o \\infty}\\frac{||x^{k+1}-x^{\\ast}||}{||x^k-x^{\\ast}||}=0\ ag{10}$ 算法（点列）是Q-次线性收敛：满足下式 $\\lim_{k\ o \\infty}\\frac{||x^{k+1}-x^{\\ast}||}{||x^k-x^{\\ast}||}=1\ ag{11}$ 算法（点列）是Q-二次线性收敛: 满足下式 $\\lim_{k\ o \\infty}\\frac{||x^{k+1}-x^{\\ast}||}{||x^k-x^{\\ast}||}\\leq a, a \\geq 0 \ ag{12}$ 不同收敛速度的是示意图如下所示。

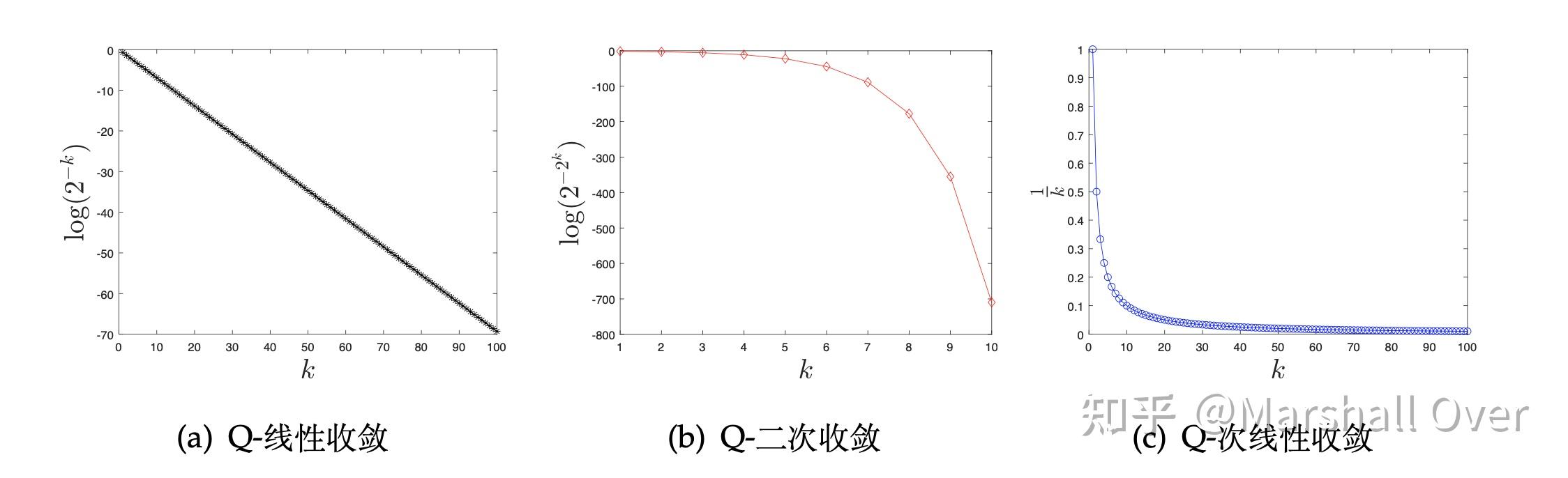
与收敛速度密切相关的概念是优化算法的复杂度，即计算出给定精度的解所需的迭代次数或浮点运算次数。注意，渐进收敛速度更多的是考虑迭代次数充分大的情形，而复杂度给出了算法迭代有限步之后产生的解与最优解之间的定量关系。

在介绍具体的最优化模型、理论和算法之前，先介绍一些必备的基础知识如范数和导数、广义实值函数、凸集、凸函数、共轭函数和次梯度等凸分析方面的重要概念和相关结论。

向量范数：称一个从向量空间到实数域的非负函数为范数，如果它满足正定性、齐次性和三角不等式，如下：

$\\begin{cases}||v||\\geq 0, ||v||=0 \\ when \\ v=0, v\\in \\mathbb{R}^n\\\\ ||\\alpha v||=||\\alpha||||v||, v\\in \\mathbb{R}^n,\\alpha \\in \\mathbb{R}\\\\ ||v+w||\\leq ||v||+||w||, v,w \\in{\\mathbb{R}^n}\\end{cases}\ ag{13}$ 常见的p范数及无穷范数定义如下：

$\\begin{cases}||v||_p=(|v_1|^p+|v_2|^p+\\cdots+|v_n|^p)^{\\frac{1}{p}}，p \\geq 1\\\\ ||v||_{\\infty}=\\mathop{\\max}_i |v_i| \\end{cases}\ ag{14}$ 对于2范数，有如下柯西不等式成立：

$|a^Tb|\\leq ||a||_2||b||_2 \ ag{15}$ 矩阵范数：和向量范数类似，矩阵范数是定义在矩阵空间上的非负函数，并且满足正定性、齐次性和三角不等式。矩阵1范数、2范数(Frobenius 范数)和核范数定义如下：

$\\begin{cases}||A||_1=\\sum\\limits_{i=1}^{m}\\sum_\\limits{j=1}^{n}|a_{ij}|\\\\ ||A||_F=\\sqrt{\\sum\\limits_{i,j}a_{ij}^2}\\\\ ||A||_{\\ast}=\\sum\\limits_{i=1}^{r}\\sigma_i, \\sigma_i \\ is \\ singular \\ vaue \\end{cases}\ ag{16}$ 矩阵内积：范数一般用来衡量矩阵的模的大小，而内积一般用来表征两个矩阵(或其张成的空间)之间的夹角，Frobenius 内积及柯西不等式定义如下：

$\\begin{cases}<A,B> \\overset{\\rm{def}}{=}\\sum\\limits_{i=1}^{m}\\sum\\limits_{j=1}^{n}a_{ij}b_{ij}\\\\ |<A,B>| \\leq ||A||_F||B||_F \\end{cases}\ ag{17}$

关于求导/微分的基础内容可参考：

https://zhuanlan.zhihu.com/p/626527733

这里主要介绍优化中常用的与导数相关的基础知识。

梯度：向量g满足下式称为函数的在x点处的梯度

$\\lim_{p \ o 0}\\frac{f(x+p)-f(x)-g^Tp}{||p||}=0 \\Rightarrow \\bigtriangledown f(x)=[\\frac{\\partial f(x)}{\\partial x_1},\\frac{\\partial f(x)}{\\partial x_2},\\cdots,\\frac{\\partial f(x)}{\\partial x_n}]^T\ ag{18}$

海森矩阵：函数f在x处的海森矩阵可以定义为

$\\bigtriangledown^2 f(x)=\\begin{bmatrix}\\frac{\\partial^2f(x)}{\\partial x_1^2}&\\frac{\\partial^2f(x)}{\\partial x_1 \\partial x_2}& \\cdots& \\frac{\\partial^2f(x)}{\\partial x_1 \\partial x_n}\\\\ \\frac{\\partial^2f(x)}{\\partial x_2 \\partial x_1}&\\frac{\\partial^2f(x)}{\\partial x_2^2}& \\cdots & \\frac{\\partial^2f(x)}{\\partial x_2 \\partial x_n}\\\\ \\cdots&\\cdots & &\\cdots \\\\ \\frac{\\partial^2f(x)}{\\partial x_n \\partial x_1}&\\frac{\\partial^2f(x)}{\\partial x_n \\partial x_2}& \\cdots &\\frac{\\partial^2f(x)}{\\partial x_n^2}\\\\ \\end{bmatrix}\ ag{19}$ 雅可比矩阵：当函数为变量x的向量值函数时，雅可比矩阵定义如下：

$J(x)=\\begin{bmatrix}\\frac{\\partial f_1(x)}{\\partial x_1}&\\frac{\\partial f_1(x)}{\\partial x_2}& \\cdots& \\frac{\\partial f_1(x)}{\\partial x_n}\\\\ \\frac{\\partial f_2(x)}{\\partial x_1}&\\frac{\\partial f_2(x)}{\\partial x_2}& \\cdots& \\frac{\\partial f_2(x)}{\\partial x_n}\\\\ \\cdots&\\cdots & &\\cdots \\\\ \\frac{\\partial f_m(x)}{\\partial x_1}&\\frac{\\partial f_m(x)}{\\partial x_2}& \\cdots& \\frac{\\partial f_m(x)}{\\partial x_n}\\\\ \\end{bmatrix}\ ag{20}$ 多元函数泰勒展开：函数连续可微，则有一阶和二阶展开如下：

$\\begin{cases}f(x+p)=f(x)+\\bigtriangledown f(x+tp)^Tp,0<t<1 \\\\ f(x+p)=f(x)+\\bigtriangledown f(x)^Tp+\\frac{1}{2}p^T\\bigtriangledown ^2 f(x+tp)p,0<t<1 \\end{cases}\ ag{21}$ 梯度利普希茨连续：可微函数满足下式称为梯度利普希茨连续

$||\\bigtriangledown f(x)-\\bigtriangledown f(y)|| \\leq L||x-y||,L>0，x,y \\in \\mathbf{dom}f\ ag{22}$ 梯度利普希茨连续表明函数梯度的变化可以被自变量x 的变化所控制，满足该性质的函数具有很多好的性质，一个重要的性质是其具有二次上界，可表示为：

$f(y)\\leq f(x)+\\bigtriangledown f(x)^T(y-x)+\\frac{L}{2}||y-x||^2,\\forall x,y \\in \\mathbf{dom}f \ ag{23}$ 矩阵变量函数的导数:多元函数梯度的定义可以推广到变量是矩阵的情形，矩阵变量函数f 在X 处Fréchet 可微，若矩阵变量G满足下式，则称G 为f 在Fréchet 可微意义下的梯度：

$\\lim_{V\ o 0}\\frac{f(X+V)-f(X)-<G,V>}{||V||}=0\ ag{24}$ 矩阵变量函数的梯度可以用偏导数表示如下：

$\\bigtriangledown f(x)=\\begin{bmatrix}\\frac{\\partial f}{\\partial x_{11}}&\\frac{\\partial f}{\\partial x_{12}}& \\cdots& \\frac{\\partial f}{\\partial x_{1n}}\\\\ \\frac{\\partial f}{\\partial x_{21}}&\\frac{\\partial f}{\\partial x_{22}}& \\cdots& \\frac{\\partial f}{\\partial x_{2n}}\\\\ \\cdots&\\cdots & &\\cdots \\\\ \\frac{\\partial f}{\\partial x_{m1}}&\\frac{\\partial f}{\\partial x_{m2}}& \\cdots& \\frac{\\partial f}{\\partial x_{mn}}\\\\ \\end{bmatrix}\ ag{25}$ Gateaux 可微: 矩阵Fréchet 可微的定义和使用往往比较繁琐，若存在矩阵G，对任意方向V满足下式：

$\\lim_{t\ o 0}\\frac{f(X+tV)-f(X)-<G,V>}{t}=0\ ag{24}$ 则称f 关于X 是Gateaux 可微的，G 称为f 在X 处在Gateaux 可微意义下的梯度。

广义实值函数：映射f满足下式，则称为广义实值函数

$f:\\mathbb{R}\\rightarrow \\overline{\\mathbb{R}},\\overline{\\mathbb{R}}\\overset{\\mathrm{def}}{=}\\mathbb{R}\\cup\\{ \\pm \\infty \\}\ ag{25}$

适当函数: 给定广义实值函数和非空集合，若满足下式，称函数关于集合是适当的：

$\\begin{cases}f(x)< +\\infty, \\exists \\ x \\in \\mathcal{R}\\\\ f(x) > - \\infty, \\forall x \\in \\mathcal{R}\\end{cases}\ ag{26}$

适当函数的特点是“至少有一处取值不为正无穷”，以及“处处取值不为负无穷”。

闭函数：闭函数是一类重要的广义实值函数，这里介绍的闭函数可以看成是连续函数的一种推广。

下水平集：满足下式，则被称为函数的下水平集

$C_{\\alpha}=\\{x|f(x)\\leq \\alpha \\},f:\\mathbb{R}\\rightarrow \\overline{\\mathbb{R}}\ ag{27}$

上方图：上方图是从集合的角度来描述函数的具体性质，满足下式则称函数的上方图：

$\\mathbf{epi}f=\\{(x,t) \\in \\mathbb{R}^{n+1}|f(x)\\leq t \\},f:\\mathbb{R}\\rightarrow \\overline{\\mathbb{R}}\ ag{28}$

上方图的一个直观的例子如下图所示，上方图将函数和集合建立了联系，函数的很多性质都可以在上方图上得到体现。

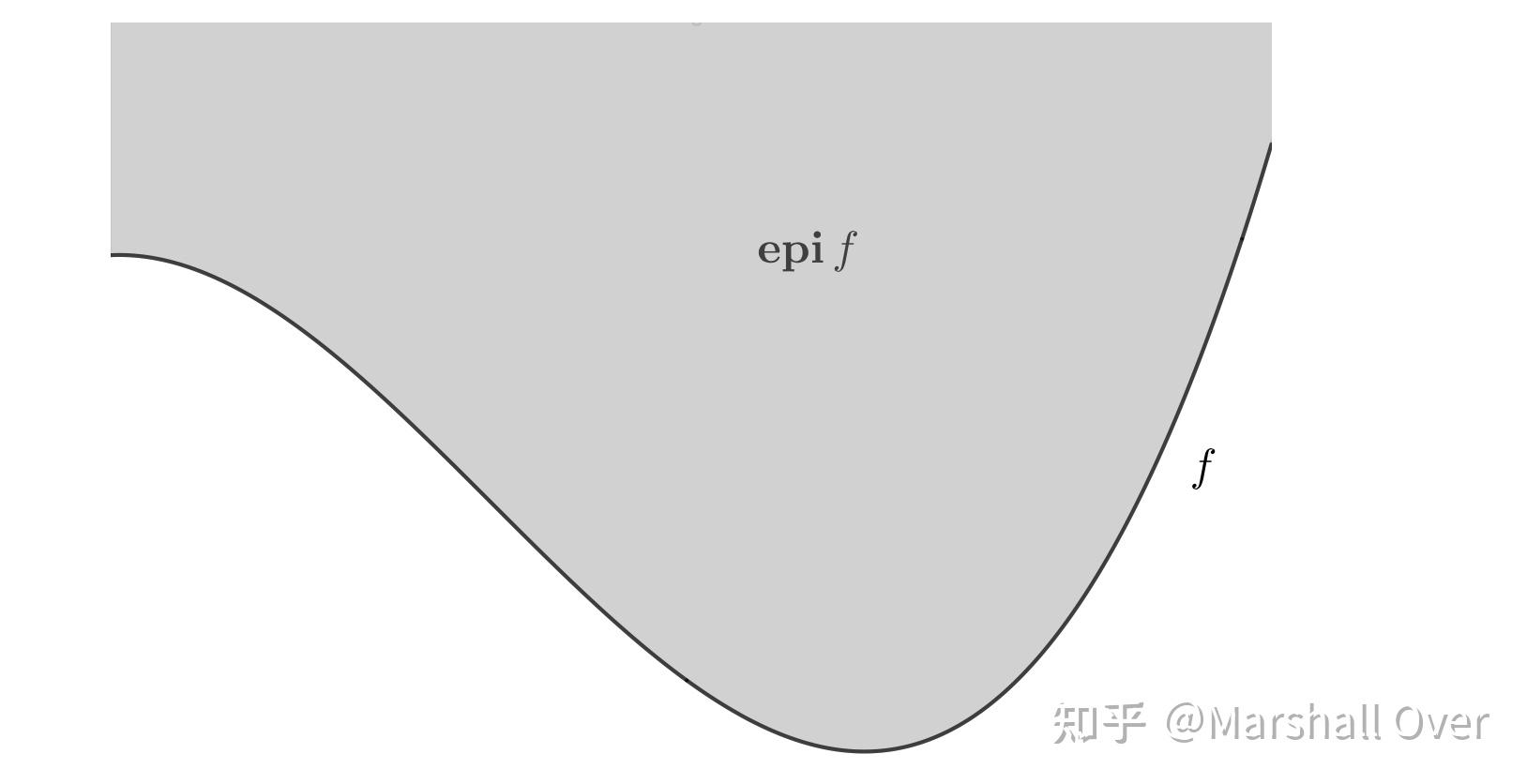
闭集：指其补集为开集的集合。另一种定义更好理解，如果一个集合包含它所有边界点，那么这个集合叫做闭集。

闭函数：若函数为广义实值函数且其上方图为闭集，则称此函数为闭函数。

下半连续函数：满足下式的函数称为下半连续函数

$\\lim_{y\ o x}\\ \\mathrm{inf}\\ f(y) \\geq f(x),f:\\mathbb{R}\\rightarrow \\overline{\\mathbb{R}}\ ag{29}$

下半连续函数示意图如下图所示。

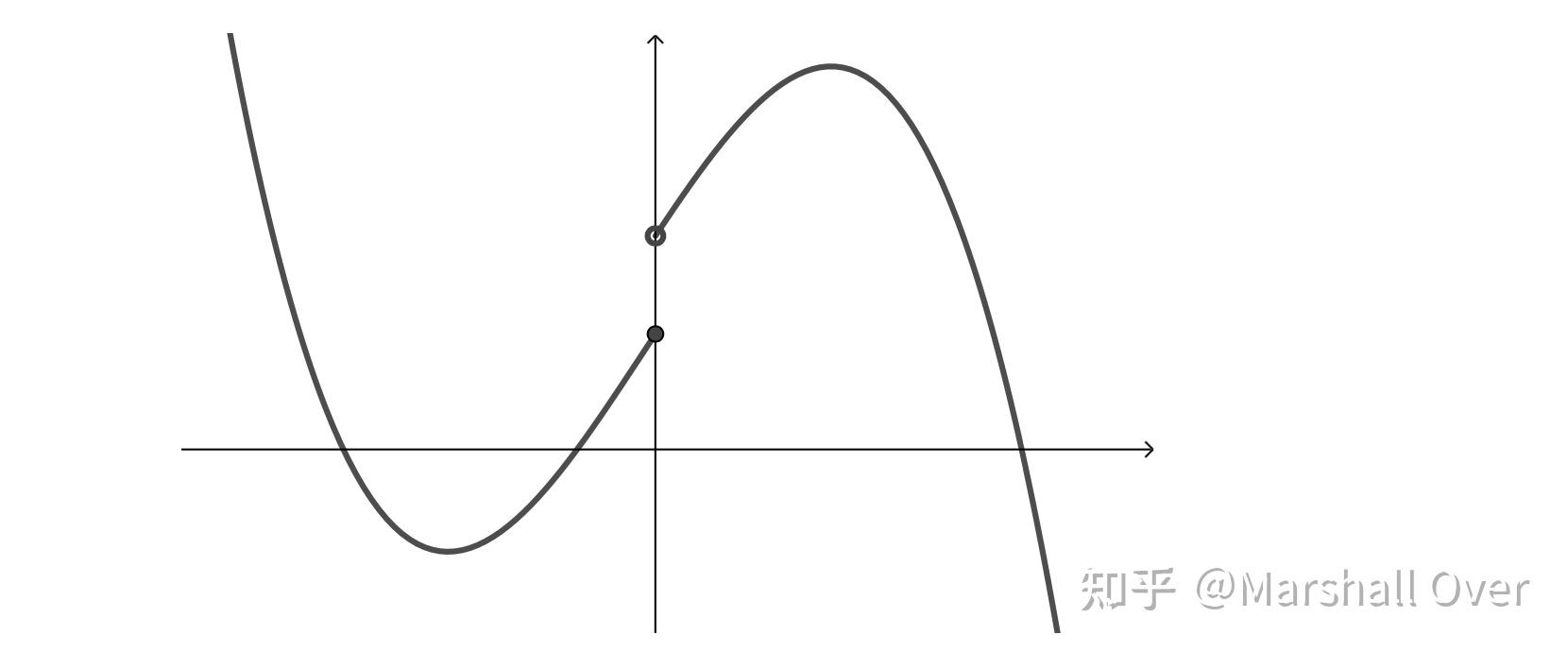
等价性：对于广义实值函数，其任意下水平集都是闭集，其是下半连续的和为闭函数，三者是相互等价命题。

仿射集：如果过集合C 中任意两点的直线都在C 内，则称C 为仿射集，即满足下式

$x_1,x_2 \\in C \\Rightarrow \ heta x_1+(1-\ heta)x_2 \\in C, \\forall \ heta \\in \\mathbb{R}\ ag{30}$

线性方程组Ax=b 的解集是仿射集。反之，任何仿射集都可以表示成一个线性方程组的解集。

凸集：如果连接集合C 中任意两点的线段都在C 内，则称C 为凸集，即

$x_1,x_2 \\in C \\Rightarrow \ heta x_1+(1-\ heta)x_2 \\in C, \\forall \\ 0 \\leq \ heta \\leq 1 \ ag{31}$

从仿射集的定义容易看出仿射集都是凸集。下面给出一些凸集和非凸集的例子。

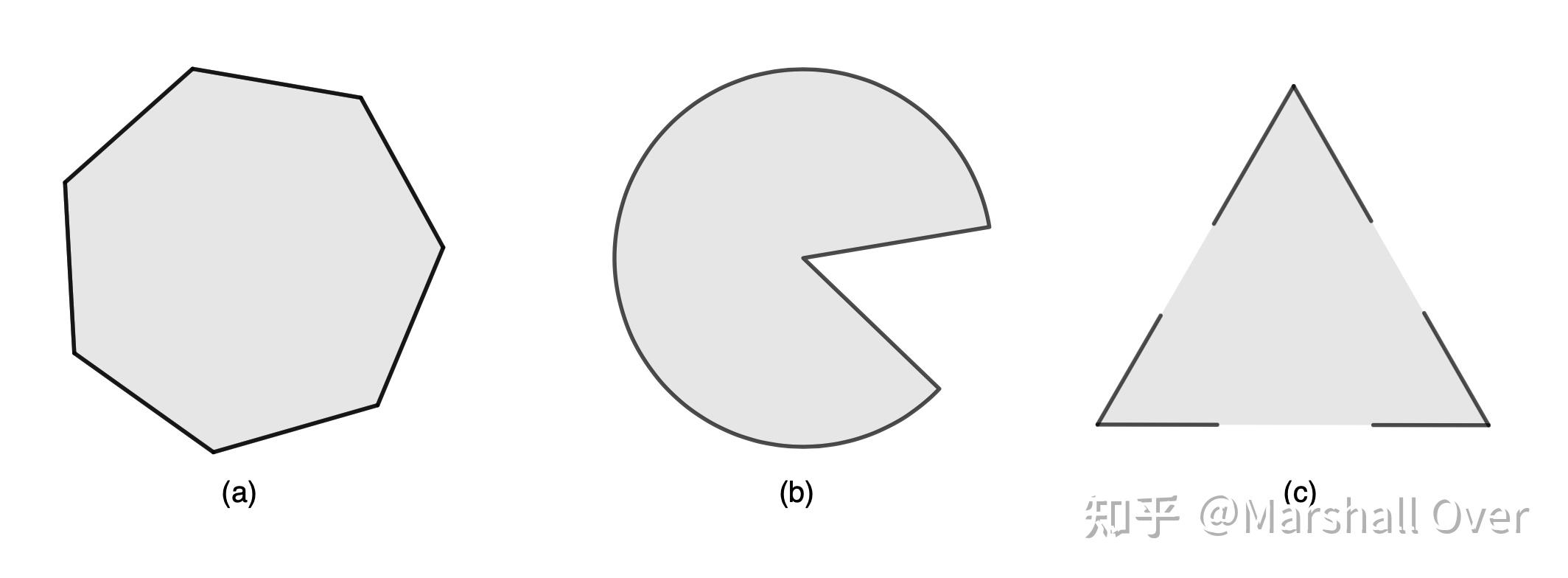
凸组合：满足下式的点称为变量的凸组合：

$\\begin{cases}x=\ heta_1x_1+\ heta_2x_2+\\cdots+\ heta_kx_k\\\\ \ heta_1+\ heta_2+\\cdots+\ heta_k=1, \ heta_i \\geq 0, i=1,2,\\cdots,k \\end{cases}\ ag{32}$

凸包：集合S 中点所有可能的凸组合构成的集合称作S 的凸包，记作conv S。conv S 是包含S 的最小的凸集。如下图所示，左边的为离散点集的凸包，右边的为扇形的凸包。

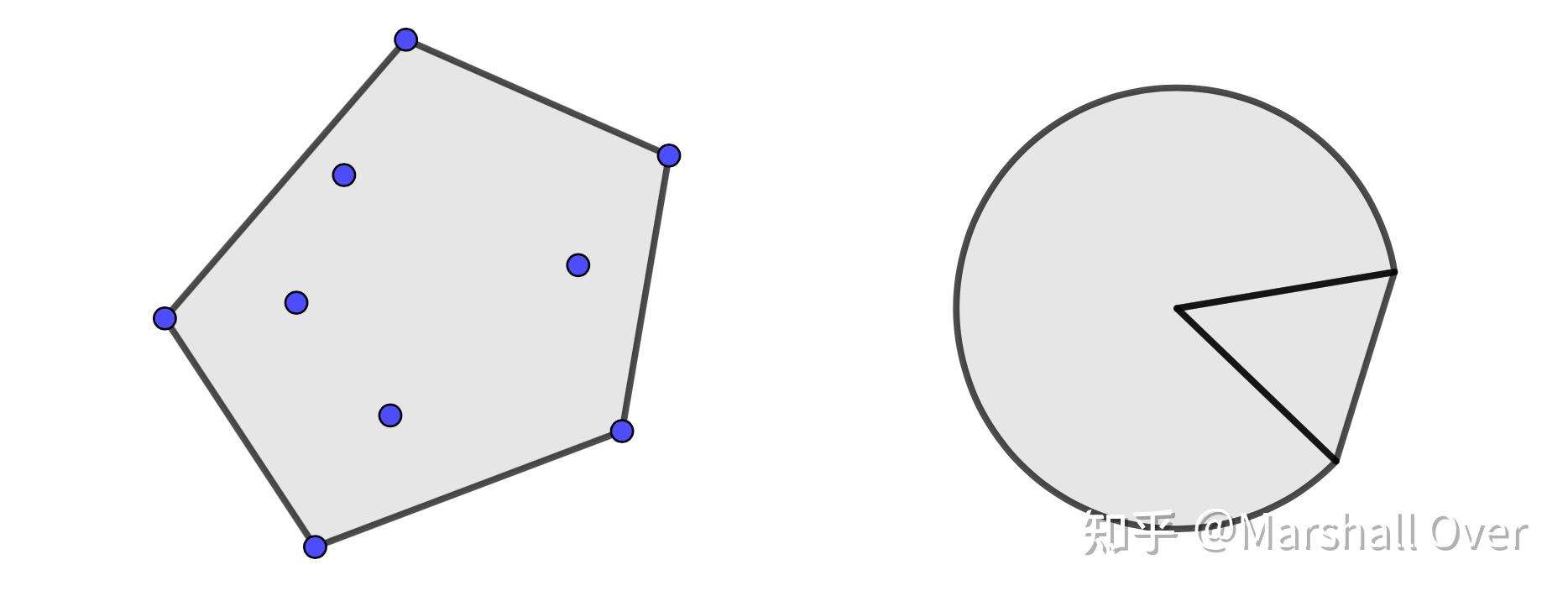
仿射包：满足下式的集合称为集合S的仿射包, 记为affine S:

$\\{x|x=\ heta_1x_1+\ heta_2x_2+\\cdots+\ heta_kx_k,x_1,x_2,\\ \\cdots x_k \\in S,\ heta_1+\ heta_2+\\cdots+\ heta_k=1\\}\ ag{33}$

下图展示了三维空间中圆盘S 的仿射包，其为一个平面。

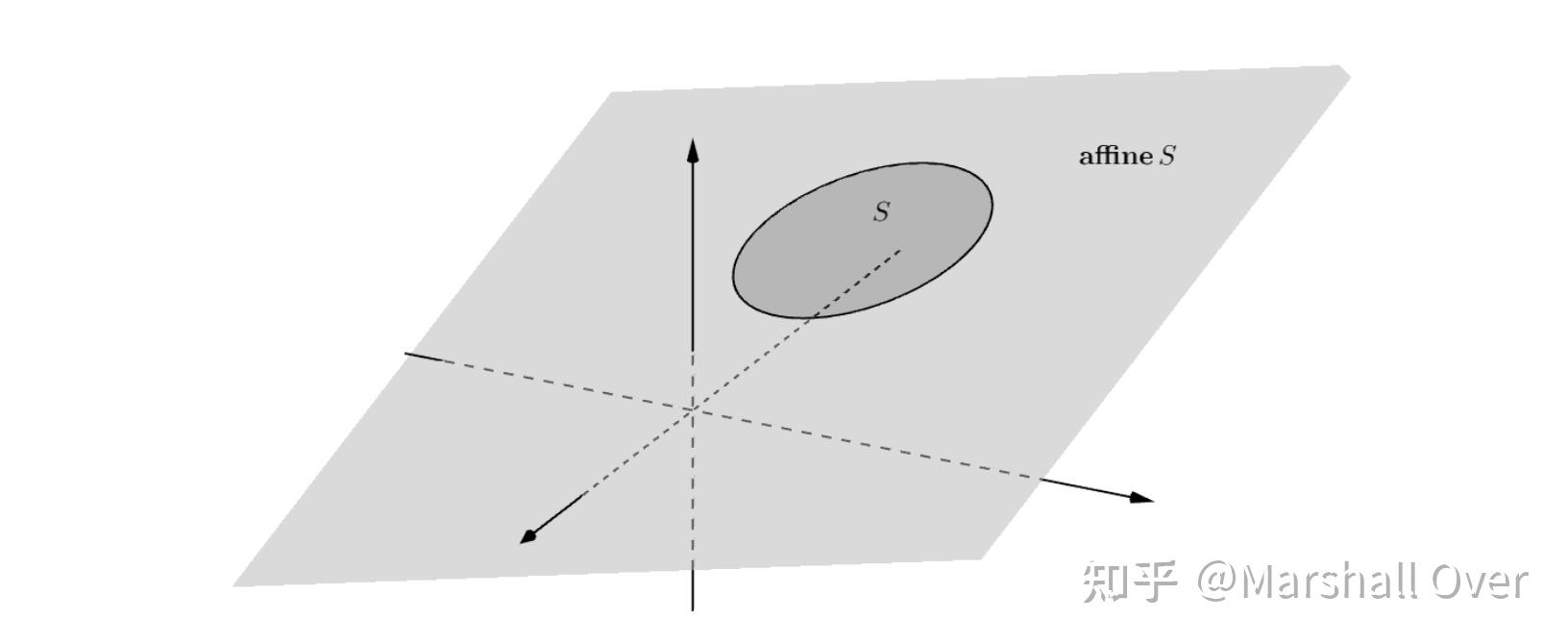
凸函数：设函数为适当函数，如果定义域为凸集，且满足下式，则称此函数为凸函数

$f(\ heta x +(1-\ heta)y) \\leq \ heta f(x)+(1-\ heta)f(y),x,y \\in \\mathbf{dom}\\ f, 0 \\leq \ heta \\leq 1 \ ag{34}$

连接凸函数的图像上任意两点的线段都在函数图像上方,如下图所示。

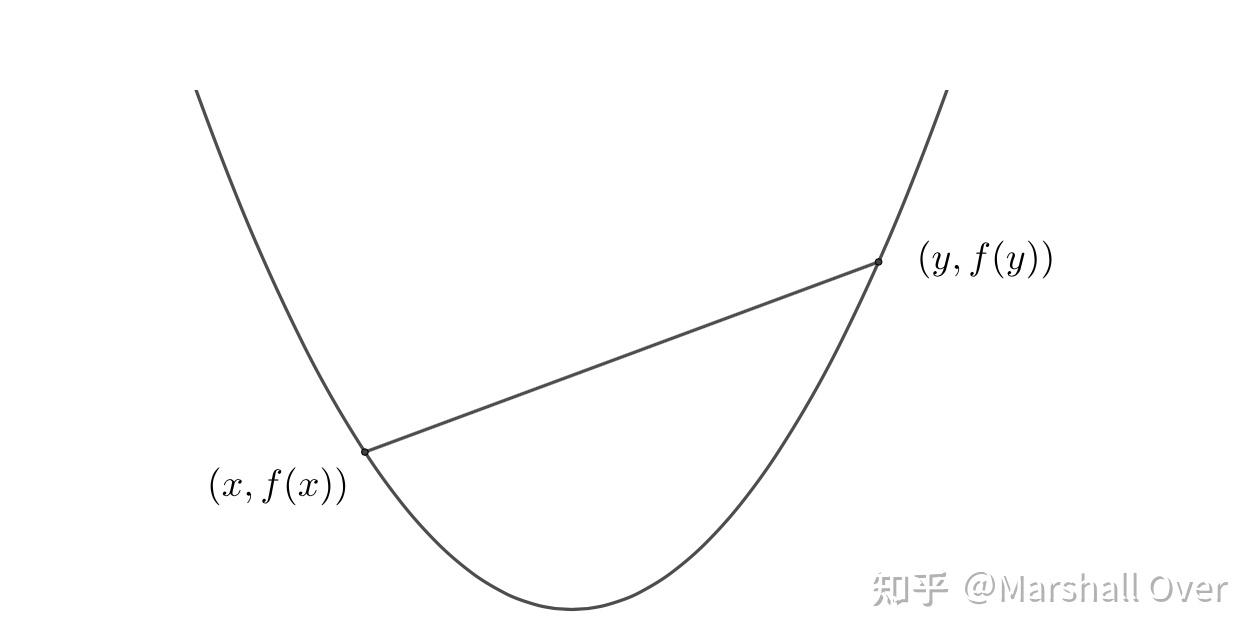
强凸函数：若存在参数，使得下式为凸函数，则称此函数为强凸函数：

$g(x)=f(x)-\\frac{m}{2}||x||^2,m >0 \ ag{35}$

性质：设函数为强凸函数且存在最小值，则其最小值点唯一。

凸函数判定定理：函数满足下式，则称此函数为凸函数

$g(t)=f(x+tv),\\mathbf{dom}\\ g=\\{x+tv \\in \\mathbf{dom}f\\},x \\in \\mathbf{dom}f,v\\in \\mathbb{R}^n,g:\\mathbb{R}\\rightarrow \\mathbb{R}\ ag{36}$

一阶条件: 对应定义在凸集上的可微函数，当且仅当下式成立，此函数为凸函数

$f(y)\\geq f(x) +\\bigtriangledown f(x)^T(y-x),\\forall x,y \\in \\mathbf{dom}f \ ag{37}$

梯度单调性：函数为可微函数，当且仅当定义域为凸集且梯度为单调映射，满足下式，则函数为凸函数。 $(\\bigtriangledown f(x)-\\bigtriangledown f(y))^T(x-y)\\geq 0, \\forall x,y \\in \\mathbf{dom}\\ f \ ag{38}$

推论：当函数为严格凸函数和强凸函数时，下式成立

$\\begin{cases}(\\bigtriangledown f(x)-\\bigtriangledown f(y))^T(x-y)> 0, \\forall x,y \\in \\mathbf{dom}\\ f \\\\ (\\bigtriangledown f(x)-\\bigtriangledown f(y))^T(x-y) \\geq m||x-y||^2, \\forall x,y \\in \\mathbf{dom}\\ f \\end{cases}\ ag{39}$ 保凸的运算: 要验证一个函数是凸函数，前面已经介绍了三种方法：一是用定义去验证凸性，通常将函数限制在一条直线上；二是利用一阶条件、二阶条件证明函数的凸性；三是直接研究函数的上方图。简单的凸函数通过一些保凸的运算得到。结论表明，非负加权和、与仿射函数的复合、逐点取最大值等运算，是不改变函数的凸性的。

凸函数性质：凸函数不一定是连续函数，但凸函数在定义域中内点处是连续的；凸函数的所有下水平集都为凸集；强凸函数具有二次下界的性质。

共轭函数：任意适当函数的共轭函数定义为 $f^{\\ast}(y)=\\mathop{\\sup}_{x \\in \\mathbf{dom}\\ f}\\{y^Tx-f(x) \\}\ ag{41}$

固定y,上式的集合意义如下图所示：

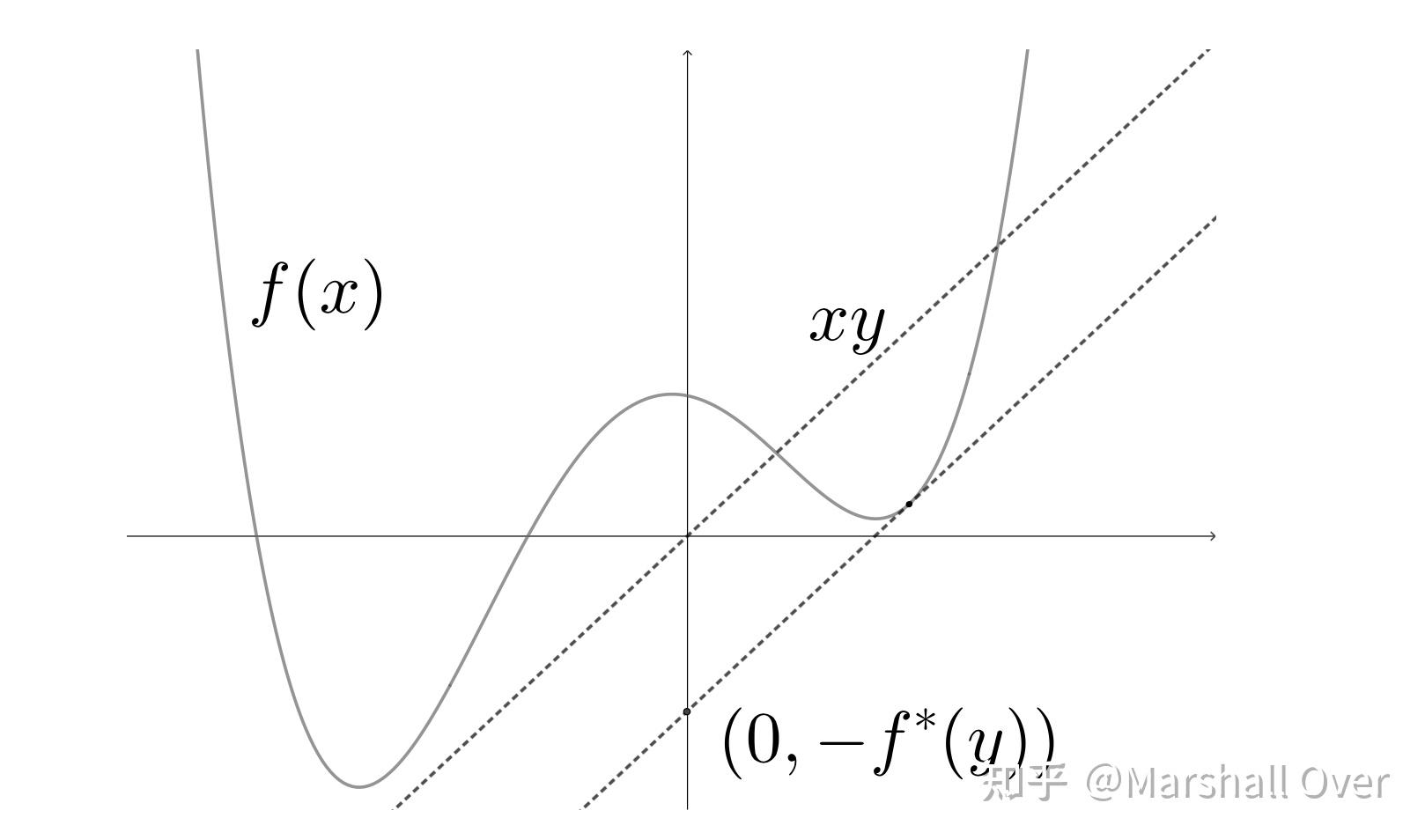
Fenchel 不等式： $f(x)+f^{\\ast}(y)\\geq x^Ty\ ag{42}$

二次共轭函数: 任一函数的二次共轭函数恒为闭凸函数。

次梯度：若函数为适当凸函数，x为定义域中一点，向量满足下式，则称此向量为函数在点x处的一个次梯度： $f(y)\\geq f(x)+g^T(y-x), \\forall y \\in \\mathbf{dom}f \ ag{43}$

次微分:下式称为函数在点x处的次微分

$\\partial f(x)=\\{g|g \\in \\mathbb{R}^n,f(y)\\geq f(x)+g^T(y-x), \\forall y \\in \\mathbf{dom}f \\}\ ag{44}$

次梯度示意图如下图所示。

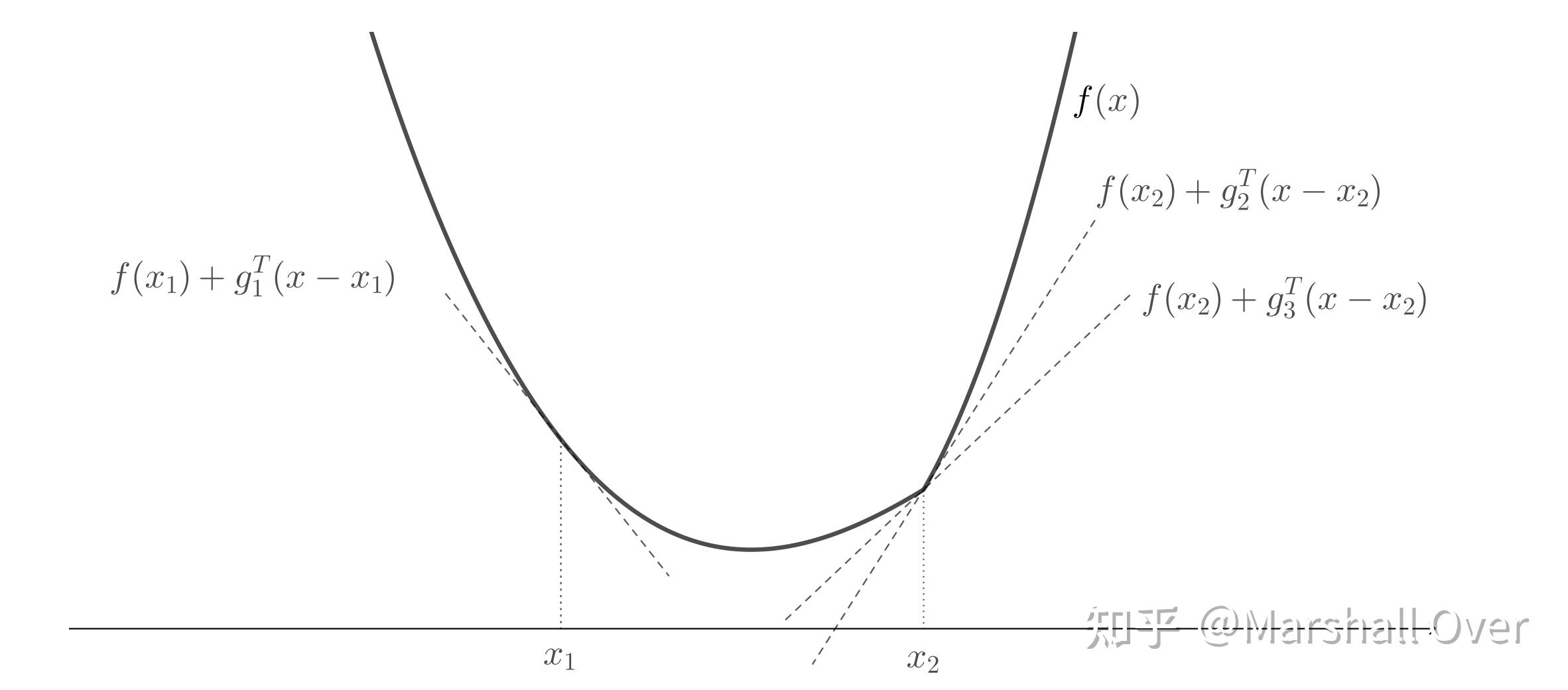
次梯度的单调性：函数为凸函数，则有

$(u-v)^T(x-y)\\geq 0, x,y, \\in \\mathbf{dom}f, u \\in \\partial f(x),v \\in \\partial f(y) \ ag{45}$

方向导数: 函数为适当函数，给定点和方向向量，方向导数(若存在)定义为

$\\lim_{t \\downarrow 0}\\phi(t)=\\lim_{t \\downarrow 0}\\frac{f(x_0+td)-f(x_0)}{t}\ ag{46}$

凸函数方向导数：函数为凸函数，给定点和方向向量，方向导数定义为 $\\partial f(x_0;d)=\\mathop{\\inf}_{t>0}\\frac{f(x_0+td)-f(x_0)}{t}\ ag{47}$

方向导数可能是正负无穷，但在定义域的内点处方向导数是有限的。

对最优化一些基本概念、基本分类和基础知识进行了介绍。

[1].刘浩洋等，《最优化:建模、算法与理论》

[2].维基百科。

上一篇: Battery Optimizer下载

下一篇: 中央美术学院和中国美术学院，究竟哪一所好？考生：看学历认可度